Compute the Tortuosity and the Diffusivity

The DiffuDict module simulates diffusion processes and post-process the simulations results to predict the tortuosity, tortuosity factor, the relative diffusivity, and the effective diffusivity of porous media.

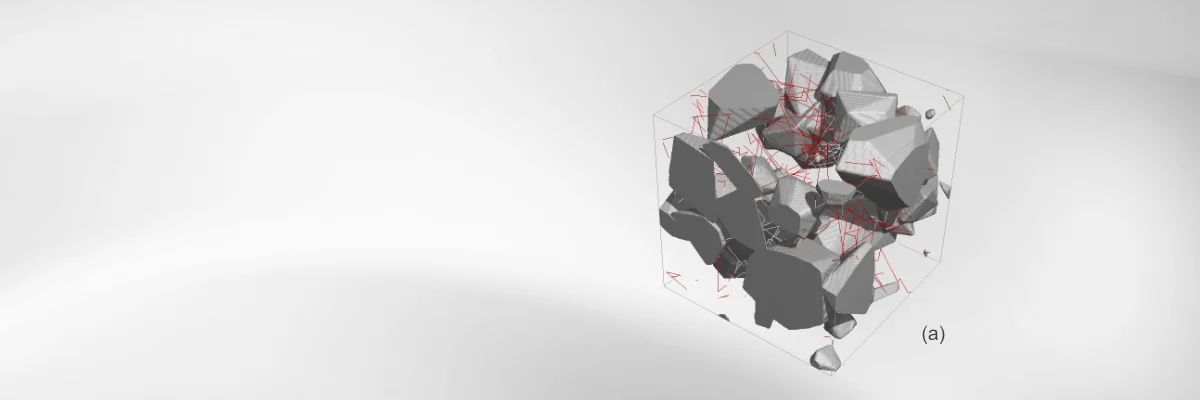
The porous media for the calculations with DiffuDict can be an imported structure from a file produced by a 3D imaging device (e.g. CT scanner or FIB/SEM) or an engineered media generated with GeoDict. Depending on the pore size, the diffusing fluid can be considered as a continuum or as discrete molecules, diffusing by reflections to the pore walls and each other.

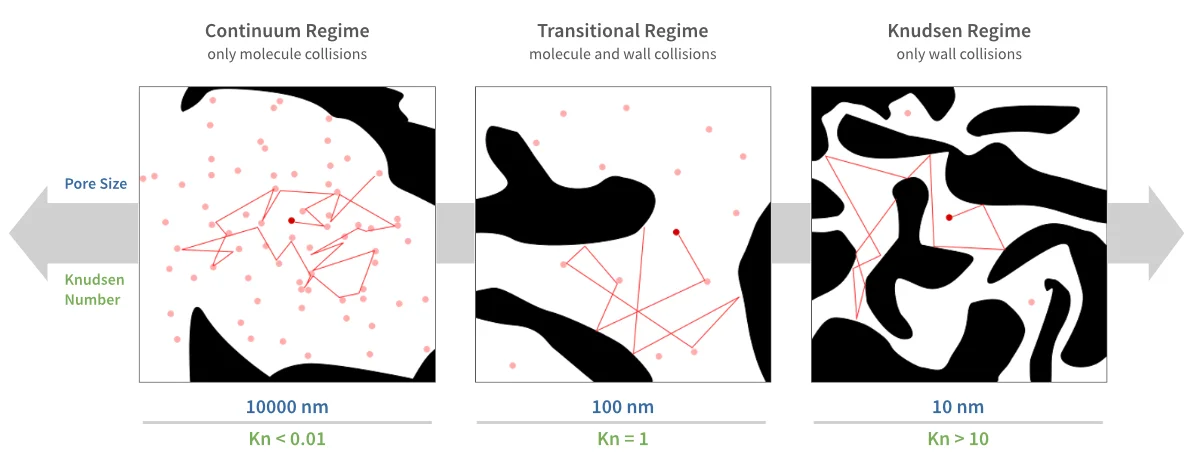
The Knudsen number (Kn), which describes the relationship between the pore diameter and the mean characteristic path length of the molecules in the fluid, determines which of both models is dominant. With large Knudsen number, the wall interaction plays the most important role for diffusion, while small Knudsen numbers denote a diffusion with primarily inter-molecular interactions.

For a Knudsen number near 1, both effects are important and can be simulated using the discrete molecule model.

• Determination of the tortuosity of pores
• Estimation of the effective diffusivity of gas diffusion layers with or without micro-porous layers
• Estimation of the relative diffusivity of the porous media
• Computation of the concentration and flux distribution inside a catalyst layer
• Computation of the porous media Knudsen number
• Determination of ion transport behavior in electrolyte or diffusion in active materials

DiffuDict predicts the tortuosity, the tortuosity factor, Knudsen number, the relative diffusivity, and the effective diffusivity of porous media. These properties can computed using different diffusion models.

The Knudsen number (Kn), which describes the relationship between the structure's characteristic length and the mean free path length of the molecules in the fluid, determines which model should be used:

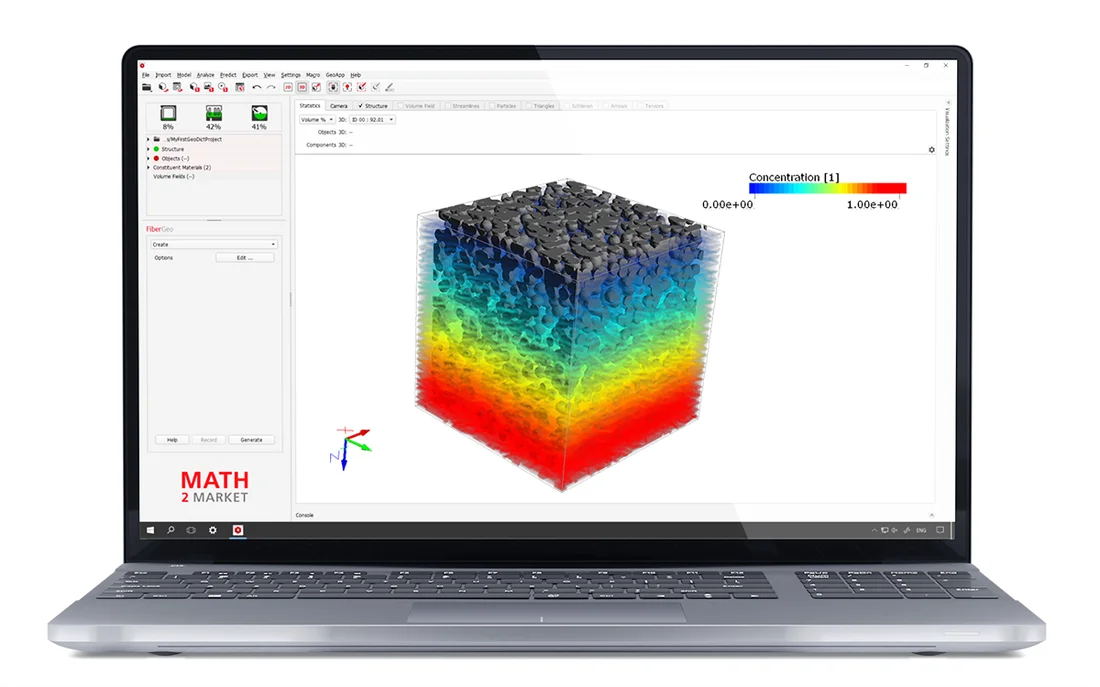
For small Knudsen numbers, the fluid is considered as a continuum and the concentration distribution inside the porous media is governed by Laplace's equation. The effective diffusivity is then determined from the resulting concentration flux applying Fick's first law. The relative diffusivity and the tortuosity factor are then found by comparing the effective diffusivity through the porous material with the bulk diffusivity inside the fluid.

The Molecular Diffusion module is designed to address the transition regime between Knudsen and Laplace/Continuum diffusion, offering a comprehensive analysis of diffusional processes. Just like for Knudsen diffusion, discrete molecule reflections at the pore walls are simulated, but additionally we consider also inter-molecular hits. The mean free path length of the gas is key parameter for the simulation of this regime.

For intermediate Knudsen numbers, Bosanquet's approximation is used to estimate the effective diffusivity by averaging between pure Knudsen diffusion and pure Laplace diffusion.

For large Knudsen numbers, the reflection of single molecules at the pore walls is simulated to obtain the mean squared displacement of the molecules over time. The effective diffusivity can be computed from this value.

The Simulate Diffusion Experiment command allows to compute a stationary diffusive flux and concentration distribution if the structure contains porous constituent materials. Diffusive properties predicted with the other commands can be used as input to compute upscaled diffusion experiments - bringing the nano-scale Knudsen diffusion results to the micro-scale.